Stability

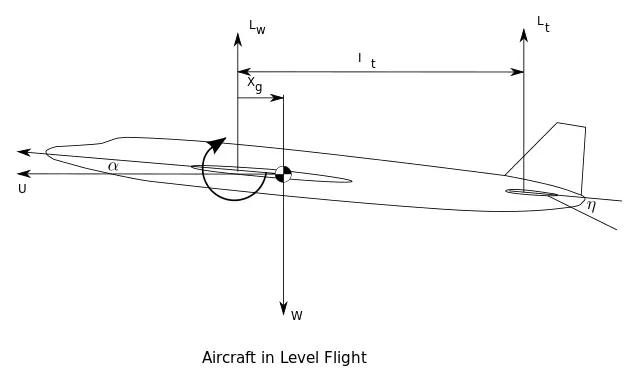
안정성 해석은 항공기 설계에 있어 매우 중요한 요소로 항공기의 성능 및 조종, 제어 기술에 직접적인 영향을 미친다. 따라서 정확한 예측이 이루어지지 않으면 항공기 개발 과정에서 많은 문제를 야기하게 된다. 일반적으로 안정성 해석은 동역학적 특성을 파악하는 것으로 동역학적 특성은 미계수의 예측을 통해 이루어진다. 항공기의 미계수는 크게 정적 미계수와 동적 미계수로 구분할 수 있다. 정적 미계수는 정적 운동변수($\alpha, \beta, \theta$ 등)에 대한 공력계수의 미분치, 동적 미계수는 동적 운동변수($\dot{\alpha}, \dot{\beta}, p$ 등)에 대한 공력계수의 미분치를 나타낸다.

미계수의 예측은 풍동시험을 통하여 예측하는 것이 일반적이다. 풍동시험에 의한 조종 및 안정성 미계수의 예측은 풍동시설의 확보와 동 안정성 미계수를 추출하는 rotary balance와 forced oscillation 시험에는 이를 위한 시험장비의 확보가 필수적이다. 또한 시험을 위한 모델제작 또한 많은 비용이 발생하게 된다. 더욱이 풍동시험으로는 kinematic constraint에 의해 동 안정성 미계수인 $C_{Lq} + C_{L\alpha}$ 의 중첩된 값밖에 얻을 수 없는 문제도 있다.

Panel 기법

패널기법인 Vortex Lattice Method를 사용할 수 있다. 이 기법은 1980년대 계산 코드가 개발되었고 1984년, Levin이 비정상 Vortex Lattice Method를 이용하여 미계수를 계산하였다. CFD에 비해서 정확도는 떨어지지만 격자생성이 쉽고 해석시간이 짧다는 장점이 있어 초기 설계에 유용하다.

CFD를 통한 기법

반면 Euler코드를 통한 CFD 방법은 Euler방정식을 직접 해석하는 방법이기 때문에 해석시간이 많이 소모되지만 패널기법에 비해 그 정확도가 높다. 본 연구실에서는 주로 동 안정성 미계수 예측시에 항공기에 강제조화진동운동을 주어 해석하였다. 이 기법은 비정상 해석으로 계산시간이 오래 걸리고 위의 풍동시험과 마찬가지로 동 안정성 미계수가 중첩된 값인 $C_{Lq} + C_{L\alpha}$ 형태로 계산되지만 풍동시험과 직접적인 비교가 가능하고 정확도가 높은 미계수를 예측할 수 있다는 장점이 있다.

또한 항공기에 적용된 좌표축에서 일정한 회전율을 갖는 경우 정상해를 갖는다는 점에 착안하여 정상해법을 통한 미계수를 예측하는 계산법을 적용하였다. 이 기법은 시간이 강제조화진동운동을 주어 예측하는 기법보다 시간이 매우 적게 걸리고 분리된 미계수인 $C_{Lq}$ 를 얻을 수 있다는 장점이 있다.